
|
Pre-Process Tab |

Script Tabs |
Post-Process Tab |

|
 Process Tab
Process TabThe Process tab is an object type-specific tab in which the processing commands of AE's scripting language are stored.
Object: Job
Object class: Executable object
Object
type (short name): JOBS
The script is either processed at job activation or start. This point in time depends on the Generate-at-runtime setting which can be defined in the Attributes tab.
Processing commands that should be processed in the header (such as setting specific host attributes) or executed before the Job Messenger starts, must be defined in the Pre Process tab.
Processing commands that should be processed after the job has ended are stored in the Post Process tab. In doing so, you can influence the final end of this job.
These lines correspond to the particular JCL (Job Control Language) of the target system and are transferred to the target system exactly as they are. DATA lines can, for example, contain BS2000 commands or MS DOS commands for batch processing.
Special Functions for Guardian/NSK
Special functions are provided for theautomated handling of input requests.
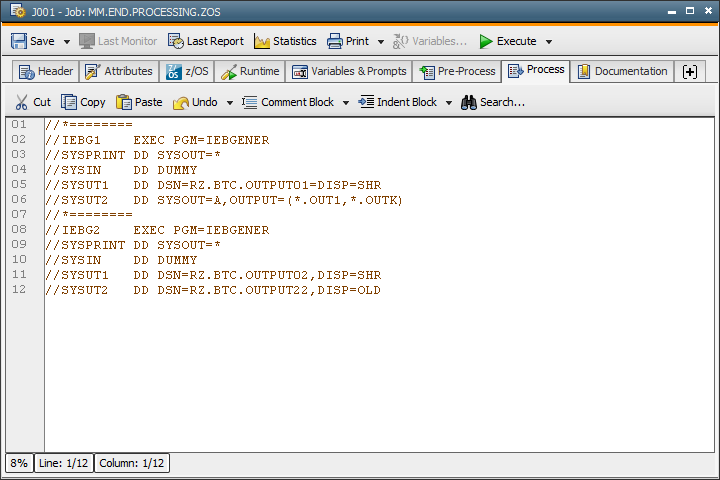
JCL for z/OS
The actual JCL is indicated here. Do NOT specify a job card (to be specified through the attributes) or an end card.
SAP JCL Interpreted By the SAP Agent
Because there is no JCL in SAP, AE supplies a SAP JCL which is interpreted by the SAP agent and converted to processing statements for the target system.
Enabling an Interpreter for Windows
You may also enter a script for use with an external interpreter. To enable the interpretation of that script, use :BEGIN_EXT_INTERPRETER and :END_EXT_INTERPRETER
In addition the Storage object's binary files may be attached and transferred to the Windows agent, using the Script function :ATTACH_RES to attach and transfer these binary files.
For details on using these functions see the respective topics.
In order to use these functions, you have to configure the variables UC_EXT_INTERPRETERS_WINDOWS and :REGISTER_VARIABLE.
Enabling an Interpreter for UNIX
The same condition as above applies to UNIX: You may enter a script for use with an external interpreter. To enable the interpretation of that script, use :BEGIN_EXT_INTERPRETER and :END_EXT_INTERPRETER
In addition the Storage object's binary files may be attached and transferred to the UNIX agent, using the Script function :ATTACH_RES to attach and transfer these binary files.
For details on using these functions see the respective topics.
In order to use these functions, you have to configure the variables UC_EXT_INTERPRETERS_UNIX and :REGISTER_VARIABLE.
Windows BAT and Powershell Examples
The Windows BAT script below puts the output of the C:\Temp directory into a file and checks whether the command ran successfully. If the command does not complete successfully, the job will end with the return code from the dir command:
dir C:\temp /S >> C:\temp\test.txt
@set retcode=%errorlevel%
@if NOT %ERRORLEVEL% == 0 goto :retcode
The Windows Powershell script below gets content of the C:\Temp directory and puts the output into a file. Then the error code from Powershell will be checked and if is not equal to 0, the job aborts with $LastExitCode, which is the equivalent to %ERRORLEVEL% in the CMD.EXE/.BAT script.
Get-ChildItem C:\Temp > C:\Temp\test.txt
if( $LastExitCode -ne 0 )
{ __uc_return $LastExitCode }
The __uc_return function is provided in the HEADER.WINDOWS include object and can be used for ending of Powershell jobs.
See also:
Script Editor
About AE Scripts
Sample Collection
REGISTER_VARIABLE.* - Register Variables or External Interpreters